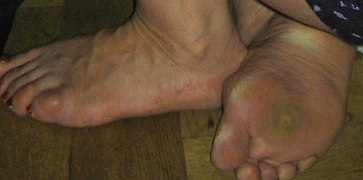
Plantar wart
| Plantar wart | |
|---|---|
| Other names | Verruca myrmecia, verruca plantaris[1] |
 | |
| Close up image of a large plantar wart | |
| Specialty | Dermatology, Podiatry |
| Symptoms | Skin colored lesion, may be painful[2] |
| Complications | Trouble walking,[2] transmission to other parts of the body, callus formation |
| Duration | Two years[2] |
| Causes | Human papillomavirus (HPV)[2] |
| Risk factors | Communal showers and pools, barefoot walking, open footwear, prior warts, poor immune function[2][3] |
| Diagnostic method | Based on symptoms[3] |
| Differential diagnosis | Callus, molluscum contagiosum, squamous cell carcinoma[2] |
| Treatment | Salicylic acid, chemo-based Fluorouracil and bleomycin,[4] cryotherapy, surgical removal[2] |
| Frequency | Common[5] |
A plantar wart is a wart occurring on the bottom of the foot or toes.[5] Its color is typically similar to that of the skin.[2] Small black dots often occur on the surface.[5] One or more may occur in an area.[2] They may result in pain with pressure such that walking is difficult.[2]
They are caused by the human papillomavirus (HPV).[2] A break in the skin is required for infection to occur.[2] Risk factors include use of communal showers, having had prior warts, and poor immune function.[2][3] Diagnosis is typically based on symptoms.[3]
Treatment is only needed if it is causing symptoms.[3] This may include salicylic acid, cryotherapy, chemo-based fluorouracil or bleomycin, and surgical removal.[2] The skin atop the lesion should generally be removed before treatment.[2] In about a third to two-thirds of cases, they go away without specific treatment, but this may take a few years.[2] Plantar warts are common.[5] Children and young adults are most often affected.[3]
Signs and symptoms
[edit]Their colors are typically similar to that of the nearby skin.[2] Small, black dots may occur on their surfaces.[5] One or more may occur in an area.[2] They may result in pain with pressure such that walking may be difficult.[2]
-
A plantar wart: striae (fingerprints) go around the lesion.
-
Mosaic wart cluster
-
Young plantar warts
-
30-year-old plantar wart
-
Deep, painful plantar warts
-
Deep plantar wart on heel
Cause
[edit]Plantar warts are benign epithelial tumors generally caused by infection by human papillomavirus types 1, 2, 4, 60, or 63,[6] but also by types 57,[7] 65,[8] 66,[9] and 156.[10] These types are classified as clinical (visible symptoms). The virus attacks compromised skin through direct contact, possibly entering through tiny cuts and abrasions in the stratum corneum (outermost layer of skin). After infection, warts may not become visible for several weeks or months. Because of pressure on the sole of the foot or finger, the wart is pushed inward and a layer of hard skin may form over the wart. A plantar wart can be painful if left untreated.[11][12]
Warts may spread through autoinoculation, by infecting nearby skin, or by contaminated walking surfaces. They may fuse or develop into clusters called mosaic warts.[6]
Diagnosis
[edit]A plantar wart is a small lesion that appears on the surface of the skin and typically resembles a cauliflower, with tiny black petechiae (tiny hemorrhages under the skin) in the center. Pinpoint bleeding may occur when these are scratched. Plantar warts occur on the soles of feet and toes. They may be painful when standing or walking.[citation needed]
Plantar warts are often similar to calluses or corns, but can be differentiated by close observation of skin striations. Feet are covered in friction ridges, which are akin to fingerprints of the feet. Friction ridges are disrupted by plantar warts; if the lesion is not a plantar wart, the striations continue across the top layer of the skin. Plantar warts tend to be painful on application of pressure from either side of the lesion rather than direct pressure, unlike corns (which tend to be painful on direct pressure, instead).[citation needed]
Prevention
[edit]HPV is spread by direct and indirect contact from an infected host. Avoiding direct contact with contaminated surfaces such as communal changing rooms and shower floors and benches, avoiding sharing of shoes and socks and avoiding contact with warts on other parts of the body and on the bodies of others may help reduce the spread of infection. Infection is less common among adults than children.[12]
As all warts are contagious, precautions should be taken to avoid spreading them. Recommendations include:
- Cover them with an adhesive bandage while swimming
- Wear latex swimming socks
- Wear flip-flops when using communal showers
- Do not share towels.[13]
Plantar warts are not prevented by inoculation with HPV vaccines because the warts are caused by different strains of HPV. Gardasil protects against strains 6, 11, 16, and 18, and Cervarix protects against 16 and 18, whereas plantar warts are caused by strains 1, 2, 4, and 63.[dubious – discuss]
Treatment
[edit]| First-line therapy | Over-the-counter salicylic acid |
| Second-line therapy | Prescribed 60% salicylic acid, intralesional immunotherapy |
| Third-line therapy | Fluorouracil cream, cryotherapy, laser therapy |
| Fourth-line therapy | Bleomycin injection, surgical excision |

A number of treatments have been found to be effective.[14] A 2012 review of different treatments for skin warts in otherwise healthy people concluded modest benefit from salicylic acid, and cryotherapy appears similar to salicylic acid.[15]
Medications
[edit]Salicylic acid, the treatment of warts by keratolysis, involves the peeling away of dead surface skin cells with keratolytic chemicals such as salicylic acid or trichloroacetic acid. These are available in over-the-counter products, but in higher concentrations may need to be prescribed by a physician. A 12-week daily treatment with salicylic acid has been shown to lead to a complete clearance of warts in 10–15% of the cases.[16]
Formic acid, topical, is a common treatment for plantar warts, which works by being applied over a period of time, causing the body to reject the wart.[17]
Fluorouracil cream, a chemotherapy agent sometimes used to treat skin cancer, can be used on particularly resistant warts, by blocking viral DNA and RNA production and repair.[4]
Bleomycin, a more potent chemotherapy drug, can be injected into deep warts, destroying the viral DNA or RNA. Bleomycin is notably not US FDA approved for this purpose. Possible side effects include necrosis of the digits, nail loss, and Raynaud syndrome. The usual treatment is one or two injections.[18][19]
Immunotherapy, as intralesional injection of antigens (mumps, candida or trichophytin antigens USP), is a wart treatment that may trigger a host immune response to the wart virus, resulting in wart resolution. It is now recommended as a second-line therapy.[20]
Surgery
[edit]
Liquid nitrogen and similar cryosurgery methods are common surgical treatments, which act by freezing the external cell structure of the warts, destroying the live tissue.[citation needed]
Electrodesiccation and surgical excision may produce scarring.[citation needed]
Laser surgery is generally a last resort treatment, as it is expensive and painful, but may be necessary for large, hard-to-cure warts.[21]
Cauterization may be effective as a prolonged treatment. As a short-term treatment, cauterization of the base with anesthetic can be effective, but this method risks scarring or keloids. Subsequent surgical removal, if necessary, also risks keloids and/or recurrence in the operative scar.[22]
References
[edit]- ^ James, William D.; Berger, Timothy G.; et al. (2006). Andrews' Diseases of the Skin: clinical Dermatology. Saunders Elsevier. p. 405. ISBN 978-0-7216-2921-6.
- ^ a b c d e f g h i j k l m n o p q r s Vlahovic, TC; Khan, MT (July 2016). "The Human Papillomavirus and Its Role in Plantar Warts: A Comprehensive Review of Diagnosis and Management". Clinics in Podiatric Medicine and Surgery. 33 (3): 337–53. doi:10.1016/j.cpm.2016.02.003. PMID 27215155.
- ^ a b c d e f Ferri, Fred F. (2017). Ferri's Clinical Advisor 2018 E-Book: 5 Books in 1. Elsevier Health Sciences. p. 1375. ISBN 9780323529570.
- ^ a b Salk, Robert S.; Grogan, Kirk A.; Chang, Thomas J. (May 2006). "Topical 5% 5-Fluorouracil Cream in the Treatment of Plantar Warts: A Prospective, Randomized, and Controlled Clinical Study". Journal of Drugs in Dermatology. 5 (5): 418–24. PMID 16703777.
- ^ a b c d e "Plantar Warts". AOFAS. Archived from the original on 11 November 2017. Retrieved 11 November 2017.
- ^ a b Human Papillomavirus at eMedicine
- ^ Egawa K, Kitasato H, Honda Y, Kawai S, Mizushima Y, Ono T (1998). "Human papillomavirus 57 identified in a plantar epidermoid cyst". Br. J. Dermatol. 138 (3): 510–4. doi:10.1046/j.1365-2133.1998.02135.x. PMID 9580810. S2CID 19998825.
- ^ "Human Papillomaviruses Compendium" (PDF). Los Alamos National Laboratory. Retrieved 2013-02-05.
- ^ Davis MD, Gostout BS, McGovern RM, Persing DH, Schut RL, Pittelkow MR (2000). "Large plantar wart caused by human papillomavirus-66 and resolution by topical cidofovir therapy". J. Am. Acad. Dermatol. 43 (2 Pt 2): 340–3. doi:10.1067/mjd.2000.100534. PMID 10901717.
- ^ Chouhy D, Bolatti EM, Piccirilli G, Sánchez A, Fernandez Bussy R, Giri AA (2013). "Identification of human papillomavirus type 156, the prototype of a new human gammapapillomavirus species, by a generic and highly sensitive PCR strategy for long DNA fragments". J. Gen. Virol. 94 (Pt 3): 524–33. doi:10.1099/vir.0.048157-0. hdl:11336/4852. PMID 23136368.
- ^ Warts, Plantar at eMedicine
- ^ a b "Understanding Plantar Warts". Health Plan of New York. Retrieved 2007-12-07.
- ^ "Clinical Knowledge Summaries: Previous version – Warts (including verrucas)" (PDF). National Health Service. January 2007. p. 2. Archived from the original (PDF) on 2011-06-01. Retrieved 2010-12-05.
- ^ Bacelieri R, Johnson SM (2005). "Cutaneous warts: an evidence-based approach to therapy". Am Fam Physician. 72 (4): 647–52. PMID 16127954.
- ^ Kwok, Chun Shing; Gibbs, Sam; Bennett, Cathy; Holland, Richard; Abbott, Rachel (12 September 2012). "Topical treatments for cutaneous warts". Cochrane Database of Systematic Reviews. 2020 (9): CD001781. doi:10.1002/14651858.CD001781.pub3. PMC 8101088. PMID 22972052.
- ^ Cockayne, S; Curran, M; Denby, G; Hashmi, F; Hewitt, C; Hicks, K; Jayakody, S; Kang’ombe, A; McIntosh, C; McLarnon, N; Stamuli, E; Thomas, K; Turner, G; Torgerson, D; Watt, I; EVerT team (September 2011). "EVerT: cryotherapy versus salicylic acid for the treatment of verrucae – a randomised controlled trial". Health Technology Assessment. 15 (32): 1–170. doi:10.3310/hta15320. PMID 21899812.
- ^ Bhat, RM; Vidya, K; Kamath, G (June 2001). "Topical formic acid puncture technique for the treatment of common warts". International Journal of Dermatology. 40 (6): 415–9. doi:10.1046/j.1365-4362.2001.01242.x. PMID 11589750. S2CID 42351889.
- ^ Soni, Prasoon; Khandelwal, Kanika; Aara, Naushin; Ghiya, Bhikam C; Mehta, Rajesh D; Bumb, Ram A (2011). "Efficacy of Intralesional Bleomycin in Palmo-plantar and Periungual Warts". Journal of Cutaneous and Aesthetic Surgery. 4 (3): 188–191. doi:10.4103/0974-2077.91250. PMC 3263129. PMID 22279384.
- ^ Champion, R. H., et al. (1998). Rook's Textbook of Dermatology. Blackwell Science, p. 1044, ISBN 0-632-06429-3
- ^ Bacelieri R, Johnson SM (2005). "Cutaneous warts: An evidence-based approach to therapy". American Family Physician. 72 (4): 647–652. PMID 16127954.
- ^ "Laser Surgery for Warts", webmd.com
- ^ Kunnamo, Ilkka (2005). Evidence-based Medicine Guidelines. John Wiley and Sons. p. 422. ISBN 978-0-470-01184-3.
External links
[edit]- Plantar warts at the Mayo Clinic website
- Warts at Merck Manual